Primer on Elliptic Curve Cryptography

I'm going to be giving a talk that gives a quick primer on elliptic curve cryptography. But I thought I'd do a writeup on it before the presentation so that people who want to read up on it before-hand can do so. That, and also writing things down actually fleshes out what I'm about to talk about.

When building information systems, you're either storing information, or sending it somewhere else. But for every interaction you have with information, malicious actors will always be attempting to either steal or sabbotage information, impersonate someone, or fraudulently deny that they have ever committed a transaction.

Our goal is to thwart these malicious actors, and the predominant strategy for this has been to have intended actors be very easily able to disseminate and store information, while making it difficult for malicious actors to cause harm.

The Discrete Log Problem (or rather the Elliptic Curve Discrete Log Problem)

There are many strategies for difficulty, but with elliptic curves (in finite fields of prime order, which is a space we will discuss a bit later), the difficulty has been brought on by the difficulty in solving the discrete log problem.

That is, we have some function that takes two parameters of a particular group (for example, two points on an elliptic curve), which returns another element of that group. We repeatedly apply that function to a single element of that group, for a very large number of times. The result of that function invocation could be public information which is potentially used to identify an actor, along with the element that the function was applied on. Meanwhile, the very large number of times where the function was applied is private information that an actor will have derived before generating that public information. Everyone knows the public information—the result of the function invocations, and the element in which the invocation was applied to—but only the actor knows how many times they've called that function to derive that public information.

To put it in math terms, let's define some function $\text{operate}$, which takes two parameters $P$ and $Q$ of a group. What we're doing is given some publicly-known information. Where element $G$, we're invoking it with some $d$ number of times:

The element $G$ along with the result $R$ is public information, but $d$ is private information that should never be shared.

The basis of the elliptic curve discrete log problem is that even if we are publicly given the element $G$, the result $R$, and the underlying algorithm behind the hypothetical $\text{operate}$ function, it should still be absolutely impossible to recover $d$.

The $\text{operate}$ function

Previously, we were introduced to the $\text{operate}$ function, which takes two elements from a group, and returns another element from that same group.

But what does it mean to operate on two elements from a group to return an element of a group, and how does it relate to elliptic curves?

In the context of elliptic curves, we have a curve that looks like the one below:

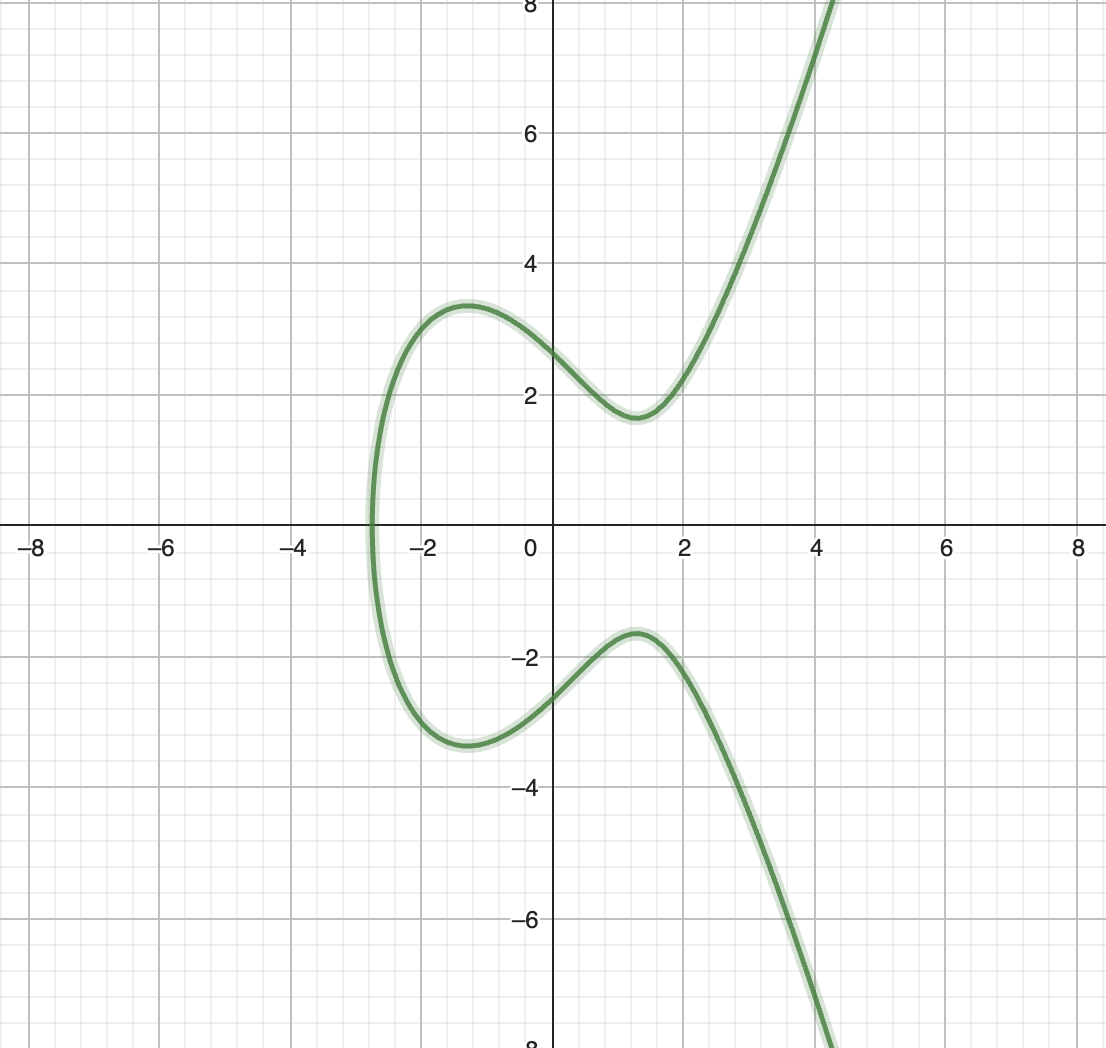
We pick two points $P$ and $Q$ on that curve, and we draw a straight line that crosses the two points, that line will actually end up crossing a third point $R'$ on the curve.

We call it $R'$ and not just $R$ is because $R'$ is not our result of our $operate$ function. Fortunately, finding $R$ from $R'$ is very easy: it's merely the result of vertically reflecting $R'$ to find $R$.

And if $P$ and $Q$ are equal to eachother (e.g. $P = Q$), then finding the result involves imagining that you are drawing a line that crosses two points that are negligibly different from each other, thus forming what is known by mathematicians a "tangent" line. And that tangent line will also cross another point, which is our $R'$, which we then flip veritcally to find $R$.

In projective geometry, the idea of counting a tangent of a line as two distinct points is called "counting multiplicities".

Just a quick spoiler: regardless of whether you decide to draw line that crosses first with $Q$ or with $P$, we will always get the same $R'$. This effectively renders the $\text{operate}$ function to have a "commutative property", that is $\text{operate}(P, Q) = \text{operate}(Q, P)$.

Later, we'll show that the the above elliptic curve rendered from the Weierstrass form $y^2 = x^3 + ax + b$ (where $a, b \in \mathbb{F}$), also shares associative properties.

Some math notations, and an introduction to Abelian groups

Earlier, I introduced the $\text{operate}$ function. But writing it out gets a little wordy.

Mathematicians have instead opted for—rather confusingly—the infix $+$ operator to express a 2-parameter operation on group elements.

That is, given two elements $P$ and $Q$ of a group, the expressed $\text{operate}(P, Q)$ operation is instead expressed as:

Yes, the $+$ symbol is used for something that may not be intuitively an addition.

It could be argued that there is a good reason for this.

For one, even with the abbreviation, repeating the expression of several "additions", $d$-number of times gets repetitive:

So, we can just express the above as a scalar multiplication of G by the quantity $d$:

The $dG$ expression is certainly a lot more compact than $\underbrace{G + G + G + \ldots + G}_{d}$.

So in short, we settled with:

Other arguments behind why is that a lot of cryptographic primitives form an Abelian group.

That is, they have the following properties:

• Commutativity: the expression $A + B$ can equally be expressed as $B + A$
• Associativity: regardless of if you compute $(A + B) + C$ or $A + (B + C)$, the results will be the same
• Existence of an identity element: given some element $I$, we can compute $A + I = A$
• Existence of an inverse: that is, not only do we have some $A$, but also some $A'$, such that $A + A' = I$. And in the case of Abelian groups that attempt to allude to the concept of an "addition", rather than expressing $A + A'$, we'd express $A - A = I$, analogous to a subtraction.

In the context of elliptic curve group operations (called "addition" going forward), the identity element isn't left to some variable name of $I$, of course. That will be discussed later.

Abelian group scalar multiplications

Earlier I mentioned that we are computing some $dG$ such that we are repeatedly applying $G + G + G \ldots G$, all the way until $G$ has been added $d$ number of times.

The problem is that $d$ can be a ridiculously large number. Sometimes a number so large, by some estimates, it exceeds the total number of atoms in the known universe!

If computers are really bad at iterating over the number of atoms in a glass of water, there is no way we're going to be able to compute a number as large as the total number of atoms in the unverse, or anything near it!

Good thing is, Abelian groups have an associative property.

Thanks to this, we can group operations together.

For example, in the expression $G + G + G + G$, rather than computing $((G + G) + G) + G$, instead, let's compute $(G + G) + (G + G) = 2G + 2G = 4G$.

When we first compute the left set of additions $2G$, we already know the value of the second $2G$, thus saving us a computation.

And we can boadly apply this to eight additions.

This should yield just 3 computations rather than 8.

The double and add algorithm

We see that there is potential to cutting down computations from $O(d)$ to just $O(log_2d)$.

But the algorithm above implies that we're using something similar to dynamic programming. That is, to memoize individual results.

This requires $O(log_2d)$ of auxiliary space.

We can do better. We can reduce that down to just $O(1)$ auxiliary space.

This is where the double and add algorithm comes in.

The basic gist of the algorithm is this:

• start with some identity element as the result $R$
• convert the number $d$ into binary digits, and iterate through each digits from most-significant bit, down to the last significant bit
  • if the digit $1$ is encountered, set $R$ to $2R + G$
  • otherwise set $R$ to $2R$

Now you've saved time from $O(d)$ down to $O(log_2d)$, with no auxiliary space required.

Possible Side-Channel attack

So with the double and add algorithm, we see that one branch of the if-statement runs two operations, where as the other only computes one.

Problem is, someone can be snooping in on CPU cycles and use it to recover the secret number!

A mitigation to the side-channel attack is to resort to the Montgomery ladder.

Why is it easy to go one way but hard the other

It's easy to go one way because we're able to look at the binary structure of an integer, but going the other way is effectively a really difficult search problem, and there are just no (known) shortcuts.

Math of drawing lines across elliptic curves

I introduced the curve, that we call the "elliptic curve". But of course, it's difficult to draw such a curve perfectly. Not to mention, computers can't work with drawings very well.

Instead, they can work with math.

They have support for additions, subtractions, exponentiation, etc.

So let's use good old math for this.

Elliptic curves can be expressed as the equation:

That equation describes what is known as a "Weierstrass form", which knowing this name may be useful when discussing ECC.

Of course $x$ and $y$ are variables that relate to eachother, but $a$ and $b$ are constants that we pick right before we interact with others.

Regardless, now our problem is, if we happened to have picked two points $P$ and $Q$ on a curve, how would we find the $x$-coordinate of the third point, and the corresponding $y$-coordinate?

Here is where we will do some derivations for the math to recover those values.

Projective Geometry

In high school, when drawing two parallel lines, both will remain parallel forever.

This is called affine geometry.

However, with elliptic curves as used in cryptography, we're going to be taking advantage of another branch of geometry called projective geometry.

Projective geomoetry shares all the same properties of affine geometry, but one important facet of projective geometry that we're going to take advantage of is that parallel lines are not parallel in projective geometry.

Instead, they intersect at a point, and that point is the point at infinity.

We'll see later that this is a powerful concept that we can take full advantage of.

Finding the x-coordinate of the third point

Let's define $P = (x_1, y_1)$ as a point on the curve and $Q = (x_2, y_2)$ on that same curve.

We'll first need to define the equation of the line that is secant to $P$ and $Q$, and it will be this:

Where we can think of $m$ as the slope of the line, and $d$ is where the line intercepts at the y-coordinate, when $x = 0$, or simply known as the "$y$-intercept".

Our $m$ isn't just any value; it's dependent on the positions of $P$ and $Q$, for $P \neq Q$, and $Q \neq -P$. To compute the slope, it's merely the "rise over the run", or rather the rate of change of $y$, with respect to $x$. In other words, it's a ratio, and the ratio is computed by calculating the differences in the y coordinates with respect to the x-coordinates.

So:

To find the $y$-intercept $\beta$, we'd simply sample a point on the equation of the line, and solve for $d$. We'll just take the coordinates from $P$.

OK, this is nice to know and all, but what can we do with this?

Well, we need to find the third point on the curve.

Can we use algebra for this?

We can see that both the equation of the line, and the equation of the curve have a $y$-coordinate.

How about we do a substitution? After all, the points on the line intersect with the points of the curve. Does this mean that both the line and the curve will intersect at all three points? Let's try:

We can see that the left-hand side is quadratic with respect to x, and the right-hand side is cubic. Subtracting a quadratic from a cubic will still yield a cubic equation.

Let's do that.

Now, here is a property that you have to remember: for cubic polynomials—such as the one that we derived on the right-hand side of the equation above—there are three possible values of $x$ that we can plug in for the equation to hold (e.g. the cubic polynomial to equal zero).

Let's call them $x_1$, $x_2$, and $x_3$.

We're getting close. We already know $x_1$ and $x_2$. Now all we need to do is find $x_3$.

Let's reinterpret the polynomial from above into some other polynomial where we re-express the constant coefficients of the polynomial as some other set of constants:

Where $a_3 = 1$, $a_2 = m^2$, $a_1 = (a - 2m\beta)$, $a_0 = (b - \beta^2)$.

We can infer this from factorizing the cubic expression like so:

Expanding the right-hand side of the above equation should yield:

Now, from the earlier derivation of our polynomial, we saw that the coefficient associatd with $a_3$ is just $1$, so we can simply get rid of the $a_3$

That is:

And also, remember, that above polynomial should equal to the one we derived earlier.

Now let's focus on the second term of both of the polynomials. We see that the second term are equal to each other.

Just get rid of the $x^2$ and the negative, and we get:

And we can finally solve for $x_3$:

Finding the y-coordinate of the third point

Finally, to solve for $y_3$, we just plug everything into the equation of the line:

What if the two points on the curve are equal to each other?

So, what if two points on the curve are equal to each other.

This would mean that if we naively plug in $m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{0}{0}$, which is indeterminate.

This means that we will need to think outside the box.

A primer on differential calculus

The trick to do is to pretend that we have a point that slightly differs on the curve, where the difference is so small, it may as well be 0, but we still get the slope of it.

I'm not going to go over the entire math behind it. But the gist of it goes like this.

Given some function $f$, we want to find the instantaneous rate of change with respect to its input.

That is, as some value $a$ approaches the input $x$ of $f(x)$, we will get the differentation at point $x$, written as $\frac{d}{dx}f(x)$, defined as the limit of $\frac{f(x) - f(a)}{x - a}$, as $a$ approaches $x$.

As a short-hand, the above can be written like so:

Alternative as some value $h$ approaches $0$, we will get the differentation at point $x$, written as $\frac{d}{dx}f(x)$, defined as the limit of $\frac{f(x + h) - f(x)}{x + h - x}$, as $h$ approaches $0$.

It can be abbreviated to:

Effectively, $\frac{d}{dx}f(x)$ is giving you the slope of some line at point $(x, f(x))$.

We're just going to go over one example, and afterwards, I'm just going to include some common patterns that have been discovered.

The beauty of the "limit" operator as denoted by $\lim_{x\rightarrow a}f(x)$ is saying that we want to know what does the expression $f(x)$ tend to as $x$ approaches $a$. We might not know much about the value at $a$, but we can give something that is pretty much the answer that we have been looking for.

This is great for functions where a function is not defined at $a$.

Let's take the function $\frac{x^2}{x}$. The function $\frac{x^2}{x}$ is indeterminate at $x = 0$, even though $\frac{x^2}{x} = x$. So, the limit expression $\lim_{x\rightarrow 0}\frac{x^2}{x}$ is saying that we are going to find some expression that $\frac{x^2}{x}$ approaches as $a$ approaches $0$. And the limit operator will help us reveal that the limit of $\frac{x^2}{x}$ as $x$ approaches $0$ is simply 0.

Now onto computing an ifinitesimally small change in x to find the slope at $x$.

Let's take the example of $f(x) = x^2$. The slope at $x$ is derived as follows:

Therefore $\frac{d}{dx}x^2 = 2x$.

There are many more rules like this.

Here's a handful of rules:

• Constant rule: $\frac{d}{dx}c = 0$
• Identity rule: $\frac{d}{dx}x = 1$
• Sum rule: $\frac{d}{dx}\sum_f^{F}f(x)=\sum_f^F\frac{d}{dx}f(x)$
• Product rule: $\frac{d}{dx}(f(x)g(x)) = f(x)\frac{d}{dx}g(x)+(\frac{d}{dx}f(x))g(x)$
• Chain rule: $\frac{d}{dx}f(g(x)) = \frac{d}{dg(x)}f(g(x))\frac{d}{dx}g(x)$

Then we can compose those above rules to create more rules.

For example, the coefficient rule is a combination of the constant rule and product rule:

And then, there is the positive integer power rule, which is just the product rule recursively applied, all the way until we reach the identity and constant rule.

I'll leave it as a exercise to prove that the positive integer power rule is pretty much $\frac{d}{dx}x^n = nx^{n-1}$, e.g. $\frac{x}{dx}x^3 = 3x^2$.

Deriving the slope of the line at a point on the elliptic curve

OK, now that we have summarized some differentiation rules above, let's go ahead and derive the equation of the curve that will help us find the slope of the line tangent to a point curve.

Recall that the equation of the curve is defined as:

Also recall that $\frac{d}{dx}f(x)$ is the slope of the point at $(x, f(x))$, pretending that we're trying to find a slope of the points $(x, f(x))$ and $(x + h, f(x + h))$, as $h$ approaches 0.

In math terms, we're looking for some $m$ such that:

In the equation of the curve, we're actually trying to find the change in $y$ with respect to $x$.

This means we're trying to find $m = \frac{dy}{dx}$.

We're going to apply the $\frac{d}{dx}$ operator on both sides of the equation.

Trying to find $\frac{dy^2}{dx}$, and then ultimately derive $\frac{dy}{dx}$ will require some clever hacks. We'll get back to it later.

Let's start with the right-hand side.

Therefore $\frac{dy^2}{dx} = 3x^2 + a$.

Now, onto the left-hand side of the equation.

What we're interested in is what happens to $y$ for some $x$. You can think of $y$ being a function of $x$.

So, we can go with chain rule.

The chain rule will give the derivative as the product of the differentation $\frac{dy^2}{dy}$ and $\frac{dy}{dx}$

So, we get $2y\frac{dy}{dx} = 3x^2 + a$.

And remember, we're trying to find $m = \frac{dy}{dx}$.

So, isolating $\frac{dy}{dx}$ from the resulting equation and we get:

What if the two points are vertical reflections of each other?

At this point, we stop.

We just assume the result is a point at infinity.

And recall that "adding" a point $P$ to a point $Q$ that is a mirror reflection of $P$ is as if $Q = -P$, and $P + Q = P + (-P) = P - P = \infty$.

Summary of elliptic curve "addition"

When two points are different, for $P = (x_1, y_1)$ and $Q = (x_2, y_2)$ the slope is simply defined as:

And for $P = Q$, then we use the derivative:

The $y$-intercept of the line is defined as:

Finally, to find the third point:

And if $Q = -P$, then we do nothing, and just have the "addition" yield the point at infinity.

Relating back to Abelian groups

Commutativity

As we can see, drawing a straight line that crosses between two points $P$ and $Q$ also crosses a third point on the curve. This is true regardless of from which direction you decided to draw that line. Did you decide to have that line cross $P$ first, or $Q$ first? The result is the same! The order doesn't matter.

Associativity

What's cool about this is that we can also apply this operation with three points $P$, $Q$, and $S$.

Regardless of if you start by attempting to find some $R_1$ by first drawing a line through $P$ and $Q$, or through $Q$ and $S$, after you've drawn a line through $R_1$ and the remaining point where you didn't "add" yet, you'll still get the same $R_2$.

Not convinced?

Stay tuned for the proof.

Identity element

This is where Mathematicians used their imagination.

It may sometimes be emphasized that $P$ and $Q$ shouldn't be vertical reflections of each other?

What happens if they are?

The resulting line will never intersect anywhere on the curve in affine geometry, but instead will intersect at a point at infinity in projective geometry, which we will denote as $\infty$.

It may sound blasphemous, but there is an important opportunity for us here.

For one, we can treat this as the "identity element".

Imagine if $P$ and $Q$ were indeed vertical reflections of each other.

Then computing $P + Q$ will give us $\infty$.

How can we use the fact that there exists some $\infty$ that we can play around with?

Well, imagine if we have $P$, and draw a perfectly vertical line that crosses $P$.

It will of course go on for $\infty$. We can think of this as $P + \infty$. Now, the thing about crossing $P$ and $\infty$, it will also cross some point that is a reflection of $P$.

And remember the operation: the idea is, once we've crossed a third point, we reflect vertically!

This means that crossing $P$ and $\infty$ will cross the vertical reflection of $P$, which we will call $P'$, and doing so will require flipping vertically, thus giving us $P$ again.

This means that $P + \infty$ yield $P$, or $P + \infty = P$.

Existence of an inverse

I've already mentioned earlier that if $P$ and $Q$ were vertical reflections of each other, then we get some point at infinity denoted as $\infty$. In other words $P + Q = \infty$, only if $P$ and $Q$ are vertical reflections of each other.

But if $P + \infty = P$, is there a $P - P = \infty$?

Yes!

If $P$ is a vertical reflection of $Q$, then this merely means that $Q$ could simply be denoted as $-P$.

In other words, "negation" is merely the act of vertically reflecting $P$.

Bonus: Proof of Associativity

Commutativity is obvious: regardless of which direction you start to draw the line between $P$ and $Q$, you will always land on the same point $-(P + Q)$.

But associativity is a bit more tricky.

For many, it's not enough to look at a drawing and be satisfied by the associative properties. Is there a case for some $P$, $Q$, and $R$, such that $(P + Q) + R \neq P + (Q + R)$?

Fortunately, we have proof that this will not be the case.

Using Bezout's Theorem

Given two polynomials of degrees $m$ and $n$, then they will intersect at exactly $mn$ points (counting multiplicity), and no more unless they have a component in common.

If we are to draw lines that are the result of summing $(A + B) + C$, we see that it yields 3 lines, and all 3 lines will intersect at exactly 9 points.

Likewise for $A + (B + C)$.

If we are to treat both sets of lines as curves on a projective plane, then both sets of lines can be thought of as cubic polynomials, and all of them will intersect at exactly 9 points, including the points crossing $(A + B) + C$ and $A + (B + C)$.

Using Cayley-Bacharach theorem

Given three points $P$, $Q$, and $R$ on an elliptic curve, we aim to show that $(P+Q)+R=P+(Q+R)$.

To prove associativity, we will utilize the Cayley–Bacharach theorem, which asserts that for any cubic curve over an algebraically closed field, if the curve passes through any eight points, it also passes through a ninth point (counting multiplicities), including the point at infinity.

Consider the set of points: $R$, $P + Q$, $P$, $Q$, $−(P + Q)$, $Q + R$, $−(Q + R)$, and the point at infinity. Suppose we construct two lines: one passing through $P$ and $Q$ intersecting the curve again at $P+Q$, and another passing through $Q$ and $R$ intersecting the curve again at $Q + R$. By reflecting these sums $P + Q$ and $(Q + R)$ about the curve, we obtain points $−(P+Q)$ and $−(Q+R)$.

These intersections provide us with two groups of lines whose intersections with the cubic yield eight distinct points (considering each pair of points contributes an intersection). By the Cayley–Bacharach theorem, any cubic passing through these eight points must also pass through a ninth point, which is exactly where $(P+Q)+R$ intersects the curve, and also where $P+(Q+R)$ intersects.

If these points were different, the sets would intersect at a tenth distinct point, violating Bézout's theorem, which states that a line and a cubic can intersect at no more than three points. Thus, we conclude that $(P+Q)+R=P+(Q+R)$, proving associativity.

How the Cayley-Bacharach theorem work

By Bezout's Theorem, we're effectively saying that two cubics $C_1$ and $C_2$ in projective space with no common components will intersect at $9$ points (counting with multiplicity). If a $C_3$ passes through all 9 points (counting multiplicity) of the intersections of $C_1$ and $C_2$, then $C_3$ can only be expressed as the linear combination $a_1C_1 + a_2C_2 = C_3$, where $a_1,a_2 \in \mathbb{F}$, by the properties of projective geometry. That is, the degrees of freedom has been restricted to only pass through the $9$ points.

Building on this, the Cayley-Bacharch theorem further refines our understanding of these intersections. The Cayley-Bacharch theorem implies that if $C_3$ shares eight of the nine intersections of that of $C_1$ and $C_2$, then it must also pass through the ninth intersection point.

Applying this back to the intersections of 3 lines with the curve, what we're trying to do is that if we have a curve, intersect 3 lines on that curve, then constructing a third curve will necessarily require that the third curve is a linear combination of the curve and the 3 lines.

The general idea is, once the first 8 points have already been selected, the degrees of freedom that we now have is highly constrained, to the point that all three curves are linearly dependent on all 9 points.

N.B. multiple lines on a plane forms a polynomial

So earlier I seemed to have treated distinct lines as a single polynomial curve.

Is that even legal?

Yes.

We're all familiar with the equation of the line of the form $y = mx + \beta$.

But there is nothing stopping us from interpreting it as the impiclit equation $0 = mx + \beta - y$.

As we can see, that equation of the line is effectively a polynomial. What happens if we compute the product of several lines to give us a polynomial, that is for example $(m_1x+b_1)(m_2x+b_2)(m_3x+b_3) = 0$?

Well, if we are to plot out the result of the implicit polynomial, this would yield a curve that looks no different than as if all lines were entirely distinct!

Try it out yourself.

Elliptic curve in finite fields

In the above derivations, if you are familiar with high school math, you'd think that we were working with real numbers.

Yes, perhaps the math would work with real numbers.

But the math would work with whatever math there is with a concept known as "field".

Real numbers are fields.

But cryptography doesn't always work with real numbers.

What they instead work with is finite fields of prime order.

Problem: computers are really bad with real numbers

Computers are really bad with real numbers.

Yes, two CPUs implementing the exact same architecture will come up with the same exact numbers, given the same exact set of instructions, but not everyone is on the same CPU architecture. At the time of writing this, people on their laptops are often on Intel-based systems. Apple has made the push for something based on ARM. And a lot of smartphones are also on ARM-based CPUs. And not to mention, RISC-V is a new contender in the CPU architecture space.

Every one of them will give you different results.

Not to mention, different implementation details will ultimately end up yielding different results. And even small discrepancies can really throw everything off.

Solution? Work exclusively with integers?

We could perhaps ditch real numbers and aim for integers.

But here's the problem with integers: they don't have a very good definition for a multiplicative inverse.

The division problem

Before we start computing divisions of integers, we got to ask ourselves: what is a divison?

Well, as far as humans and counting is concerned, divisions is just trying to discover how many times can one number fit into another.

For example, how many times can $3$ fit into $12$? The answer is $4$.

But if we are to think strictly in terms of group theory, a divison $\frac{a}{b}$ is to take some $a$ and multiplying it by the multiplicative inverse of $b$. That is, the multiplicative inverse of $b$ is some quantity $c$ such that $bc = 1$, which is impossible with integers.

Group theory and the multiplicative inverse

Recall that in an Abelian group, we have four properties:

• Commutativity
• Associativity
• Identity element
• Inverse

With integer addition and multiplication we get commutativity and associativity. We may have an identity element with additions, but multiplications? What do we get?

Well, we still get 1, but if we are to multiply two integers $a$ and $b$, can we ever get the number $1$?

Of course, with integers this is literally impossible.

Forget real numbers; forget integers. Finite fields of prime order is here to save the day

So we just found out we may have some "identity" element with integers. But we lose the multiplicative inverse with integers. That is, there can never exist two integers $a$ and $b$ where their product will yield $1$.

This is where we ditch real numbers and the integer space, but instead work with another much smaller integer space called finite fields of prime order.

Working within a finite field means to work with integers $0$ to $p - 1$, where $p$ is a prime number.

The math with finite fields is very similar to integers and real numbers, but like elliptic curve groups, the "+" operator and—now—multiplication works slightly differently.

All operations not only give the "addition" (as intuitively understood by the act of addition, since we were taught in elementary and high school), but additions greater than equal to the prime $p$ wraps around.

For example, given some finite field with prime $p = 13$, the sum $10 + 4$ would yield $1$. The expression is similar to the integer arithmetic $(10 + 4) \text{ mod } 13 = 1$, but mathematicians prefer to "abbreviate" things using the congruence $10 + 4 \equiv 1 \text{ }(\text{mod } p)$, with—in our—$p = 13$.

With finite fields, we most certainly have Abelian group properties, for both the additive and multiplicative groups, but the multiplicative aspects also has one additional property: distributivity.

That is, $a(b + c) = ab + ac$.

Finite fields actually saving the day for multiplicative inverses

Other than distributivity, we also retain the one important property: multiplicative inverse.

That is, given some $a$, we can find some $b$ such that:

Again, this is possible, because the modulo operator forces everything to just "wrap around", and we want to find some $b$ (the multiplicative inverse of $a$) such that their products "wrap around" to the value $1$.

Notation for multiplicative inverse

In real numbers, the expression $\frac{1}{a}$ can also be expressed as $a^{-1}$.

Likewise for finite fields.

And better yet, we can express the property of the multiplicative inverse as:

$aa^{-1} \equiv a^{-1} a \equiv 1 \text{ }(\text{mod } p)$.

Modular arithmetics

OK, so I used the $\text{mod}$ operator previously.

For those not familiar with that operator, it's pretty much a facet of math that we were taught roughly around the 4th grade.

It's the idea of "division with remainder". This "4th grader math" has the fancy name "Euclidean division", which is named after the mathematician who is known for having formalized and documented it in his work.

It goes like this: take for example the division $10$ divided by $4$.

$4$ does not divide $10$.

But $4$ does fit into $10$ up to $2$ times, which would yield the number $8$. What remains is $2$.

The $\text{mod}$ operator only cares about the remainder in a Euclidean divison, which in the case of the division $10$ divided by $4$, the modulo $10 \text{ mod } 4 = 2$.

Multiplicative inverses in finite fields

OK, with finite fields, we can most certainly have an $a$ and a $b$ such that their product yields $1 \text{ }(\text{mod } p)$ (where $p$ is a prime). Such an operation is literally impossible with integers, but possible with finite fields.

But now, how do we find the multiplicative inverse?

Perhaps using the greatest common divisor ($\text{gcd}$)?

For the record, the $\text{gcd}$ function takes two integers, and attempts to find their greatest common divisor.

So, if we are to pick some integer $0 < a < p$, where $p$ is prime, then the $\text{gcd}(a, p) = 1$.

We may be onto something.

There's also Bezout's identity.

It stipulates that the $\text{gcd}(a, b)$ is the linear combination:

That is, we can find some x, and some y, such that the above linear combination holds true.

But in the case of $a$ and $p$, where—recall that—$p$ is prime, we get:

If we compute the modulo of both sides, we get

In the above equation, because $py$ is a multiple of $p$, then $py \text{ mod } p$ effectively "wraps" around to $0$.

So then

And thus

The multiplicative inverse

To find the multiplicative inverse, we can take full advantage Bezout's Identity.

Again, in modular arithmetic:

And remember $py \equiv 0 \text{ }(\text{mod } p)$ cancels out, so we're left with:

We can then use the extended Euclidean algorithm to derive Bezout's identity.

And remember, the whole idea of the multiplicative inverse is that there exists some $a$ and $b$, such that their product yields $1$. This means, using Bezout's identity, we can effectively find the multiplicative inverse quite easily.

Euclidean algorithm

Before we talk about the extended Euclidean algorithm, let's first talk about the Euclidean algorithm.

The Euclidean algorithm is just a fancy word for an algorithm that repeatedly applies the Euclidiean division between a dividend and divisor, all the way until we reach 0.

The Euclidean algorithm can be succinctly defined as the recurrence:

Extended Euclidean

We've seen a very simple algorithm to compute the greatest common denominator of two (positive) integers.

Now onto the extended Euclidean algorithm, which should help us find the coefficients $x$ an $y$ in Bezout's identity, $ax + ay = gcd(a, b)$.

If $a$ and $b$ isn't a representation of the base case (that is $b = 0$), then the above equation can also be expressed as:

But, careful, just because $gcd(a, b) = gcd(b, a \text{ mod } b)$, doesn't mean that $ax + by$ is $bx + (a \text{ mod } a)y$.

Instead, the $x$ and the $y$ are something different, so we'll use $x'$ and $y'$, that is:

So, we will need to do more algebraic manipulation to make finding $x$ and $y$ easy.

The trick would be to look at one definition of the modulo operator.

One plausible definition of the operator $a \text{ mod } b$ is

So we can rewrite the above equation representing one level below the start of the recursion as:

Now we see that

And we can see that $x = y'$ and $y = x' - \lfloor\frac{a}{b}\rfloor y'$.

Of course, the expression $ay' + b(x' - \lfloor\frac{a}{b}\rfloor y')$ doesn't really tell us much about $x$ and $y$ itself. But, we will get a good insight once we reach the base case.

Recall that going one level below the recursion to gives us $ay' + b(x' - \lfloor\frac{a}{b}\rfloor y')$ which is also equal to $bx' + (a \text{ mod } b)y'$.

We can clearly draw the parallel between $gcd = gcd(b, a \text{ mod } b)$. So not only does $\text{gcd}$ have a base case, but so will the recurrence equation.

Once we reach the base case, we'll just set $x' = 1$, and $y'$ shouldn't matter, since $b$ is equal to zero.

We're going to write some psuedopython to represent the recurrence.

We're not actually going to return some equation. Instead, we're just going to return the $x$, and $y$ coefficients.

def extended_gcd(a, b):
    if b is 0:
        return (1, 1)
    x1, y1 = extended_gcd(b, a % b)
    return (y1, x1 - (a//b)*y1)

Divisions in finite field

In real numbers, divisions are just that: divisions.

With integers, I did mention divisions become problematic when attempting to naively divide two numbers as if we were trying to divide real numbers.

For example, $\frac{10}{4}$ yields $2.5$ in real numberes, but things get awkward in integers.

Recall also that in real numbers, that there indeed exists some $a$ and $b$ such that $ab = 1$. This is because a multiplicative inverse for $a$ exists in real numbers. Nothing like that exists in integers.

And this is why we use finite fields.

Finite field math is often coupled with modular arithmetics, and modular arithmetics pretty much has things "wrap around". With the help of the extended Euclidean algorithm, when attempting to find the modular inverse of $a$, we're looking for something that when multiplied by it, the product will "wrap around" to $1$.

I've also mentioned that a notation for $\frac{1}{a}$ in real numbers is $a^{-1}$, and we can do the same in finite fields.

Better yet, many mathematicians express the congruence $aa^{-1} \equiv a^{-1}a \equiv 1 (\text{mod } p)$ (where $p$ is prime) as just

This brings us to divisions in finite field.

Divisions in finite field simply involves finding the multplicative inverse of the denominator (a.k.a. the divisor). Once found the multiplicative inverse, we take that value and multiply the "dividend" with the computed multiplicative inverse.

The cyclic group

Elliptic curves in finite field forms not only an Abelian group, that is, it satisfies the commutative, associative, identity, and inverse properties, but it also forms a cyclic group.

What it means for something to be a cyclic is that there exists some element in the group—called the Generator—such that its scalar multiplication or exponentiation yields every element in the group.

In the case of elliptic curves, given the coefficients $a$ and $b$ for the Weierstrass equation, and the prime field, there exists a finite number of points on the curve, denoted as $n$. In a lot of these curves, ther could exist one point $G$ on the curve such that for every coefficient $d$ in ${0, 1, 2, \ldots, n}$, the multiple $dG$ will yield every point on the curve. In this case, $G$ is known as the generator.

Putting it all together

We've defined the math of finding a third point on an elliptic curve. The act of flipping that "third point" on the curve vertically is the algorithm of an elliptic curve group "addition".

Now that we know about the math, let's put this all together with finite field math.

Recall that real numbers form a field.

Not only is the computation of a third point on the curve can be done in the real number field, but we can also do the same computation with finite field of prime order. Since finite fields are fields, the curve equation works perfectly with finite fields.

The only difference being that everything happens modulo a prime for the finite field, and that division isn't simply the act of finding how many times the divisor fits inside the dividend, but instead, we compute the multiplicative inverse, such that the product of the divisor $a$ by the multiplicative inverse of $a$ yield $aa^{-1} \equiv 1 (\text{mod } p)$ (where $a^{-1}$ is the multiplicative inverse, and that $p$ is prime).

Application to cryptography

Elliptic curve group arithmetic in finite field of prime order is the math that is used to take full advantage of the hardness of the solution to the discrete log problem. And because it is known to be difficult to solve (on a classical computer), it is an excellent cryptographic primitive for various cryptographic schemes in cybersecurity applications.

First thing's first: public and private keys

The discrete log problem stipulates that given some 2-parameter group operation (such the elliptic curve "addition"), given some positive integer $d$, and a group element $G$, we can compute the scalar multiplication $nG = R$, where having access to $G$ and/or $R$ is not at all adequate to find the integer $d$. In order to recover $d$, we will actually need to physically steal it.

Thus, the integer $d$ can be regarded as private information, and $G$, and $R$ can be shared publicly.

In real-world applications, $G$ is typically some standardized parameter, such as the G variable that is defined in the secp256r1 specification. Thus $G$ is never explicitly shared by either communicating parties, but instead has been agreed upon, and already known by everyone, and ahead of time.

The only thing that "belongs" to someone is the scalar multiplication $nG$. For example, Alice can generate her secret number $d_A$, and she can use it to derive $d_A G$. She would share the result of the scalar multiplication $d_A G$, but she will never share $d_A$ on it's own; it's a secret. Again, by the nature of the hardness of the discrete log problem $d_A$ can never be extracted from $d_A G$.

In the real world, $d_A$ is the private key, and $d_A G$ is the public key.

The curve parameters

When Alice and Bob wants to engage in a transaction that involves elliptic curves, it is a good idea for them to work with provably secure parameters that many applications are aware of.

Earlier I mentioned "secp256r1".

secp256r1 is an example of standard curve parameters.

It stipulates

• the order of the finite field $p$ (the prime number that represents the order of the field, which is the total number of elements in the field)
• the value of the $a$ and $b$ coefficients of the equation in Weierstrass form
• the generator point $G$

The parameters also includes numbers that would have otherwise needed to be computed, such as the order of the curve $n$–which is the total number of points on the curve, including the point at infinity.

In fact, the $n$ will be the most helpful, since it's ideal if coefficients avoid ever equaling $n$, since doing so will yield the point at infinity.

How these points are chosen

Typically, cryptographers would pick some arbitrary prime $p$, and points $a$ and $b$. Then count the total number of points on the curve to derive $n$. If $n$ is a prime, there would only ever be one cyclic subgroup, and thus one generator $G$, such that multiplying it with every value $d$ in ${1, 2, 3, \cdots n}$ will yield every point on the curve, including the point at infinity.

Next is to find some point $G$ such that $nG$ yields the point at infinity.

Thus we have our $a$, $b$, and $p$ parameters of our curve, and the derivations of the order $n$, and our generator $G$, such that $nG = \infty$.

Key exchange, for encryption

ECC isn't typically used for encryption.

That said, we can use ECC for deriving a shared secret, which is then used against a symmetric cipher, such as AES.

So we've established that extracting the scalar coefficient in an elliptic curve scalar multiplication is prohibitively difficult to do.

We've also established that ellitpic curve arithmetic forms an Abelian group, with associative properties.

This means that not only can Alice derive her public key $d_A G$, but she can then send it to Bob, so that Bob, using his private key $d_B$ can derive $d_B d_A G$. And Bob can likewise send his public key $d_B G$ to Alice, and she can then compute $d_A d_B G$.

And due to the commutative nature, $d_A d_B G = d_B d_A G$.

Both Alice and Bob should land on the same value on the Elliptic curve, and neither of them will have ever shared $d_A$ nor $d_B$, and no one can extract those values.

How shared secrets are used

Typically, once the shared curve point on an elliptic curve has been established, the $x$-coordinate of the curve point is used as the input to a key-derivation function (KDF).

Typically, the KDF used is HKDF. It has the most provable security, and it is strongly resistant against key material weakness.

For HKDF, we need some cryptographically-secure salt, and our derived $x$-coordinate from our key exchange. Once derived, we should then have a secure key, from which it is impossible to derive the shared $x$-coordinate.

The derived key and a plaintext is then input into a cipher, such as AES-256-GCM (of course, along with cryptographically-random initialization vector).

The decryptor will then take the derived key to decrypt the message.

Digital signatures

Digital signatures involves having Alice prove that she sent a message, by "signing" it using her private key, and Bob can then "verify" the signature against the message using Alice's public key.

The most widely used digital signature algorithm is ECDSA.

This is how it works.

Let's say Alice wants to send a message $m$ to Bob, and she signs it using her private key $d_A$.

Alice would send to Bob two values, represented in the following tuple:

Where $k$ is a totally random number between $1$ and $n - 1$, and $\text{HASH}$ is some hash function such as $SHA-256$.

And note: that tuple does not represent any point on the curve! $r$ and $s$ are two distinct values.

Alice sends $(r, s)$ to Bob, and when Bob wants to verify the signature using Alice's public key $Q_A$, he'd compute

Bob will absolutely know that the signature is valid if $R_x = r$

How digital signature verification works

Even though Bob has no clue about the values $k$ and $d_A$ that was used by Alice to compute how $r$ and $s$, but as long as Bob is aware of the overall algorithm, he can know how to derive $kG$, even if he doesn't know $k$.

Expanding the above $\frac{\text{HASH}(m)}{s}G+\frac{r}{s}Q_A$, we get

From the above equation, we can factor out $\frac{kG}{\text{HASH}(m)+(kG)_xd_A}$

Then the denominator cancels out parts of the nominator, and finally all we are left with is $kG$, from which, the $x$-coordinate should equal to Alice's supplied $r$.

Conclusion

Elliptic curve cryptography leverages group operations on an elliptic curve in finite fields of prime order, in projective plane geometry.

Multiplying the generator $G$ of the curve by some $d$ will yield some point $dG$ in $O(log_2n)$ time by taking advantage of elliptic curve Abelian commutative properties, without ever revealing to anyone what $d$ is. Most importantly, there are no known efficient algorithm to recover $d$ without an exhaustive search. In other words, easy to compute one way, but hard to go the other, which is the basis of most cryptosystems.

We're then able to exploit this property and use it in various cryptographic use cases. The simplest example is deriving a shared secret between Alice and Bob, by having them share each other's publicly available point on the curve, then having each of them then multiply it with their own secret number to derive the shared secret.